MEDIDAS DE ÁREA
Para transformar unidades maiores para menores, multiplica-se.
MEDIDAS DE ÁREA
Unidades de medidas de comprimento
As unidades de medidas de comprimento surgem para suprir a necessidade do ser humano de medir vários tipos de distâncias. Existem várias unidades de medidas de comprimento, a utilizada no sistema internacional de unidades é o metro, e seus múltiplos (quilômetro, hectômetro e decâmetro) e submúltiplos (decímetro, centímetro milímetro).
Os múltiplos e submúltiplos do metro são representados por siglas:
quilômetro → km
hectômetro → hm
decâmetro → dam
metro → m
decímetro → dm
centímetro → cm
milímetro → mm
Conversão das medidas de comprimento
Para realizar a conversão, precisamos construir a seguinte tabela, respeitando a ordem para os múltiplos e submúltiplos do metro:
ou seja
O que são Gráficos?
Gráficos são representações visuais utilizadas para exibir dados, sejam eles, sobre determinada informação, ou valores numéricos.
Geralmente, são utilizados para demostrar padrões, tendências e ainda, comparar informações qualitativas e quantitativas num determinado espaço de tempo.
Exemplo:
São ferramentas utilizadas em diversas áreas de estudo (matemática, estatística, geografia, economia, história, etc.) para facilitar a visualização de alguns dados, bem como para tornar os dados mais claros e informativos.
Dessa forma, o uso de gráficos torna a interpretação e/ou análise mais rápida e objetiva.
Elementos dos gráficos
Alguns elementos importantes que estão incluídos nos gráficos são:
Título: geralmente possuem um título a respeito da informação que será apresentada.
Fonte: muitos gráficos, sobretudo os da área de estatística, apresentam a fonte, ou seja, de onde as informações foram retiradas. Também podem apresentar o ano de publicação da fonte referida.
Números: estes são essenciais para comparar as informações dadas pelos gráficos. A maior parte deles utilizam números, seja para indicar quantidade ou tempo (mês, ano, trimestre).
Legendas: grande parte dos gráficos apresentam legendas que auxiliam na leitura das informações apresentadas. Junto a ela, cores que destacam diferentes informações, dados ou períodos, são utilizadas.
Exemplo:
Desmatamento na Amazônia cresce 3,8 – Em 28/11, o Instituto Nacional de Pesquisas Espaciais (INPE) informou o desmatamento na região da Amazônia indicando as áreas desmatadas a cada ano.
Gráfico de Linhas
O gráfico de linhas (ou de segmentos) é utilizado, em geral, para representar a evolução dos valores de uma variável no decorrer do tempo.
Veja alguns exemplos de gráficos de linhas a seguir:
Porcentagem
Porcentagem, representada pelo símbolo %, é a divisão de um número qualquer por 100.
Exemplos:
- A expressão 25%, por exemplo, significa que 25 partes de um todo foram divididas em 100 partes.
- Se num grupo de 100 pessoas existem 55 mulheres e 45 homens, podemos dizer que a porcentagem de mulheres é de 55%, enquanto a porcentagem de homens é 45%.
Etimologicamente, a palavra porcentagem se originou do latim per centum, que significa literalmente "por cento" ou "por cada centena".
Para quê serve a porcentagem?
É uma medida matemática que é usada a comparar grandezas e determinar descontos ou prejuízos, taxas de juros acréscimo de valores, quantidades, etc.
Todos esses cálculos estão presentes na vida cotidiana como, por exemplo, quando você ouve frases:
Há três formas de representar uma porcentagem: forma percentual, forma fracionária e forma decimal.
O cálculo do valor representado por uma porcentagem geralmente é feito a partir de uma multiplicação de frações ou de números decimais, por isso o domínio das quatro operações é fundamental para a compreensão de como calcular corretamente uma porcentagem.
Videozinho com um macete para calcular porcentagem.
EXERCÍCIOS PARA RESPONDER NO CADERNO:
Questão 1: 25 representa quantos por cento de 200?
a) 12,5%
b) 15,5%
c) 16%
d) 20%
Questão 2: 30 representa 15% de qual número?
a) 150
b) 200
c) 350
d) 400
Questão 3: Em uma sala de aula há 30 alunos, dos quais 40% são meninas. Quantas meninas têm na sala?
a) 10 meninas
b) 12 meninas
c) 15 meninas
d) 18 meninas
Questão 4: Convertendo a fração 2/5 em uma fração centesimal, qual o resultado em porcentagem?
a) 10%
b) 20%
c) 30%
d) 40%
Ligações Químicas
As ligações químicas correspondem à união dos átomos para a formação das substâncias químicas.
Os átomos se ligam para buscar estabilidade eletrônica. Segundo a teoria do octeto, a maioria do átomos (excetos H e He) se estabilizam com 8 elétrons em sua ultima camada.
Os principais tipos de ligações são:
Ligações iônicas: transferência de elétrons;
Ligações covalentes: compartilhamento de elétrons;
Ligações metálicas: existência de elétrons livres.
Também chamada de ligação eletrovalente, esse tipo de ligação é realizada entre íons (cátions + e ânions -), daí o termo "ligação iônica".
Exemplo: Na+Cl- = NaCl (cloreto de sódio ou sal de cozinha). Nesse composto, o sódio (Na) doa um elétron para o cloro (Cl) e se torna um cátion (carga positiva), enquanto o cloro torna-se um ânion (carga negativa).
Outros exemplos de substâncias formadas por ligações iônicas são:
As ligações covalentes são ligações em que ocorre o compartilhamento de elétrons para a formação de moléculas estáveis, segundo a Teoria do Octeto; diferentemente das ligações iônicas em que há perda ou ganho de elétrons.
Exemplo: H2O: H - O - H (molécula de água) formada por dois átomos de hidrogênio e um de oxigênio. Cada traço corresponde a um par de elétrons compartilhado formando um molécula neutra, uma vez que não há perda nem ganho de elétrons nesse tipo de ligação.
Outros exemplos de substâncias formadas por ligações covalentes são:
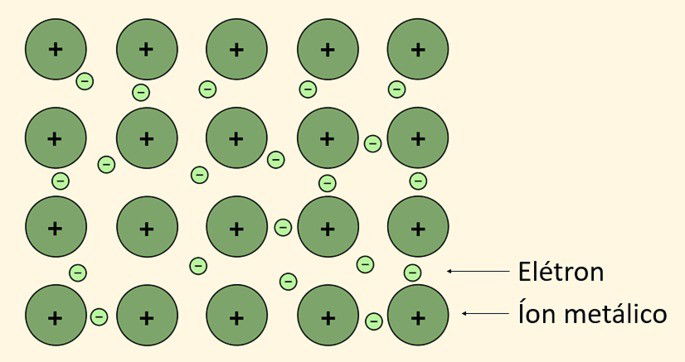
É a ligação que ocorre entre os metais, elementos considerados eletropositivos e bons condutores térmico e elétrico. Para tanto, alguns metais perdem elétrons da sua última camada chamados de "elétrons livres" formando assim, os cátions.
A partir disso, os elétrons liberados na ligação metálica formam uma "nuvem eletrônica", também chamada de "mar de elétrons" que produz uma força fazendo com que os átomos do metal permaneçam unidos.
formam as ligas metálicas presente no ouro de jóias (Au + Cu), o almágama das obturações dentárias (Hg + Ag + Sn.), no aço (Fe + C).
Exemplos de metais: Ouro (Au), Cobre (Cu), Prata (Ag), Ferro (Fe), Níquel (Ni), Alumínio (Al), Chumbo (Pb), Zinco (Zn), entre outros.
Os metais apresentam estado físico sólido em temperatura ambiente, com exceção do mercúrio, o único metal líquido nessas condições. As substâncias metálicas são boas condutoras de calor e eletricidade e, além disso, apresentam um brilho característico.
Vídeo sobre ligações metálicas:
Agora assistam ao vídeo resumindo os tipos de ligações químicas:
Para ajudar na fixação do conhecimentos trabalhados respondam ao exercício online abaixo:
Exercício - clique aqui e responda
Valeu!!
Profº Ednei